BLOCKSCAD Y LAS MATEMÁTICAS. IGNICIÓN
Taller de BlocksCAD
23/02/2019
(Presentación realizada con Reveal.js, Pandoc y Markdown)
Presentación
Pablo Beltrán Pellicer 
pabelpe@gmail.com
Carlos Rodríguez Jaso 
carlos.rodriguez.jaso@gmail.com
El proyecto
Origen: Exploración de las posibilidades matemáticas en la impresión y modelado 3D.
- BlocksCAD es un programa para modelar objetos en 3D basado en bloques
- Desarrolla el pensamiento computacional y la capacidad espacial,
Permite trabajar contenidos matemáticos, sobre todo de geometría, aunque no exclusivamente
Documentación
Toda la documentación del proyecto se encuentra liberada en Github:
- acerca de: Información del proyecto, presentaciones, enlaces a recursos, …
- actividades3d: Wiki con actividades de modelado
- mat3d.github.io: El código fuente de la página web
Si quieres colaborar, puedes ponerte en contacto con alguien del proyecto
Conociendo BlocksCAD
Acceso
- Usando la web de BlocksCAD: https://www.blockscad3d.com
- Opciones:
- Probar –> Create Now
- Registrarte en su web –> Register
- Alternativa: Crear un servidor local. Instrucciones en el repositorio Github con el código libre de BlocksCAD
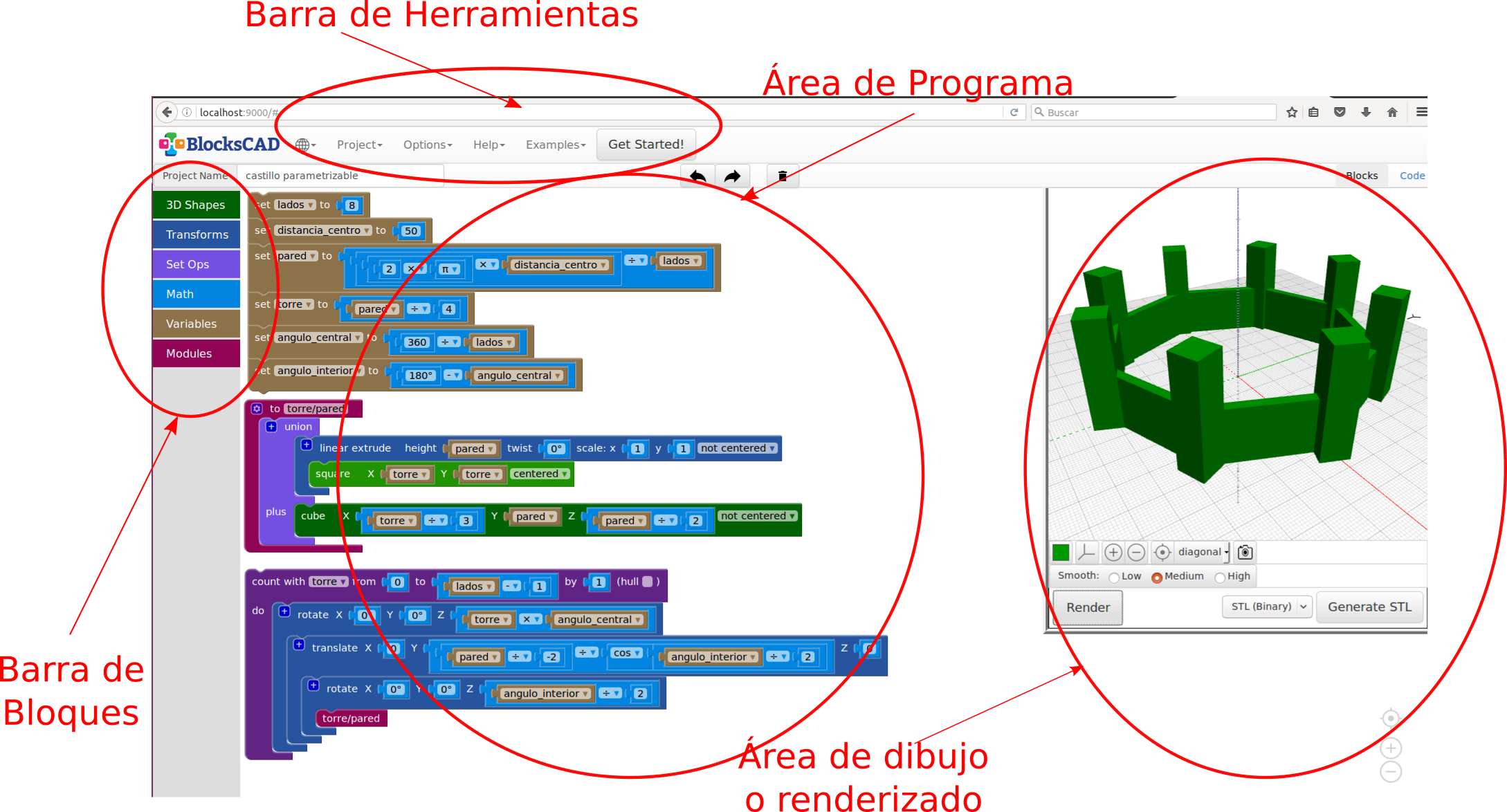
El entorno
- Barra de menús/herramientas:
- Idioma
- Proyectos
- Opciones
- Barra de bloques
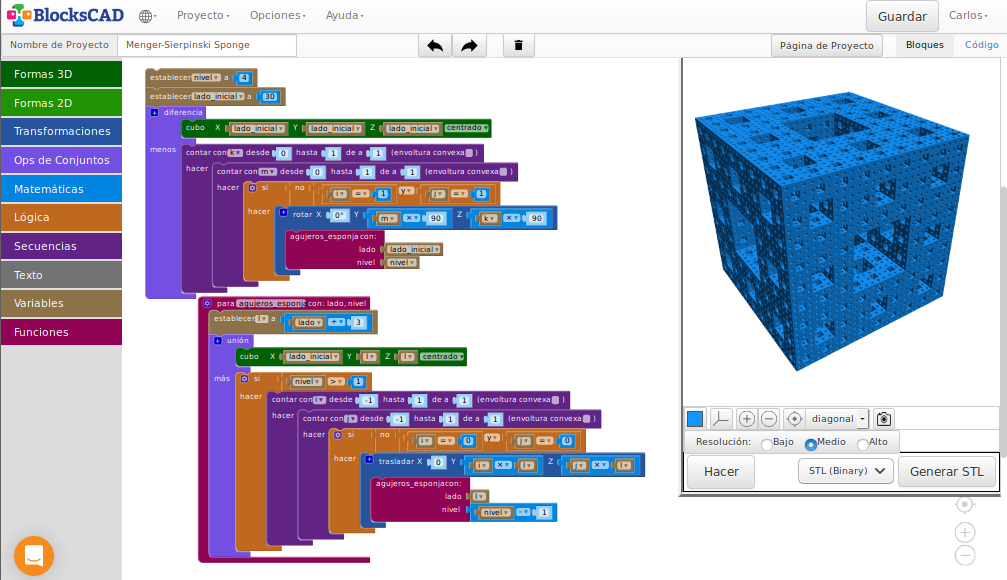
- Área de programa o proyecto: ficheros .xml
- Área de renderizado o visualización de objetos
Ya podemos empezar. Seguiremos este tutorial
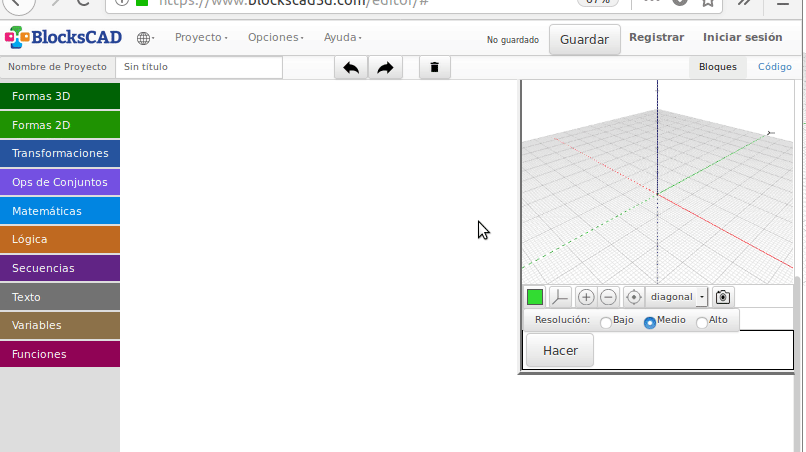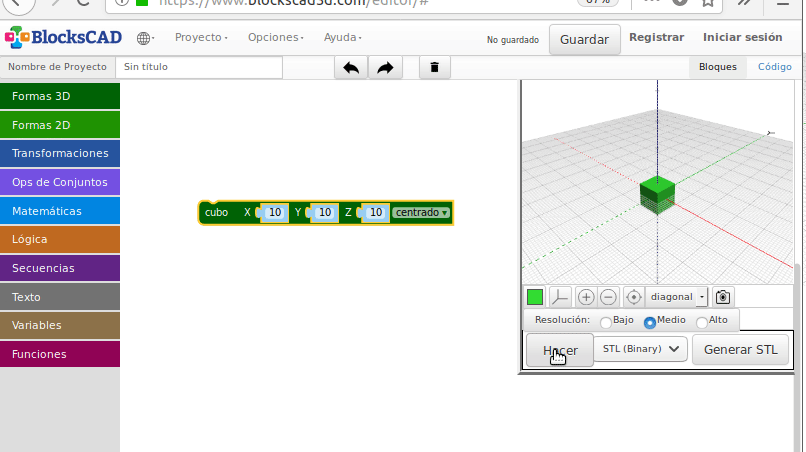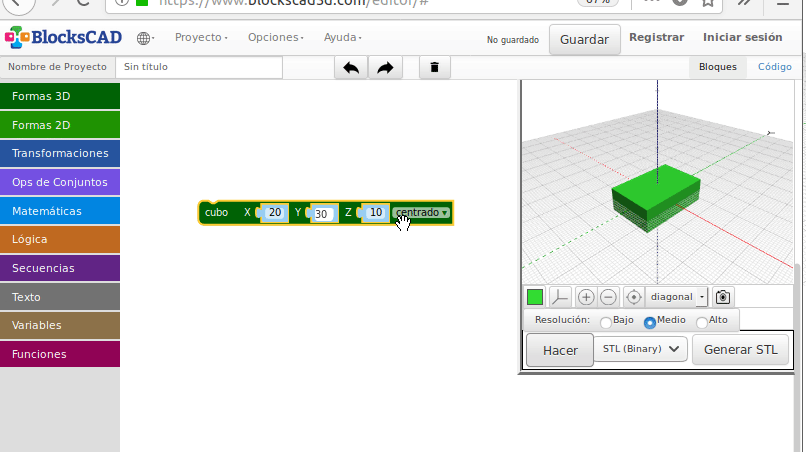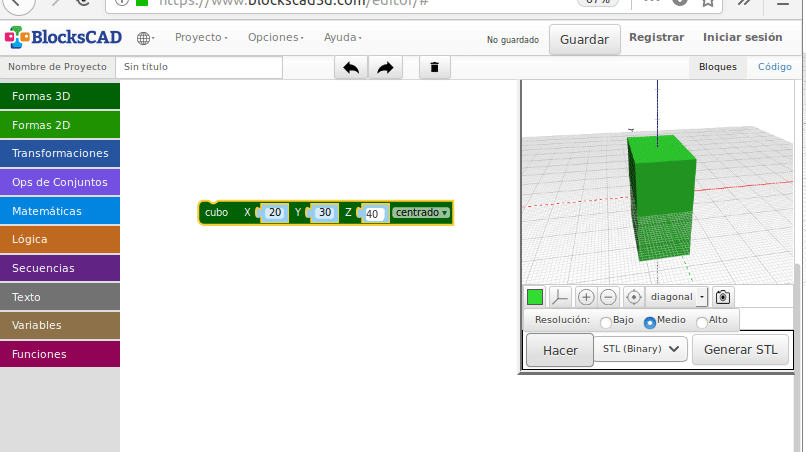
Empezamos a modelar: Cubo “Hola Mundo”
Más formas 3D
- Esferas
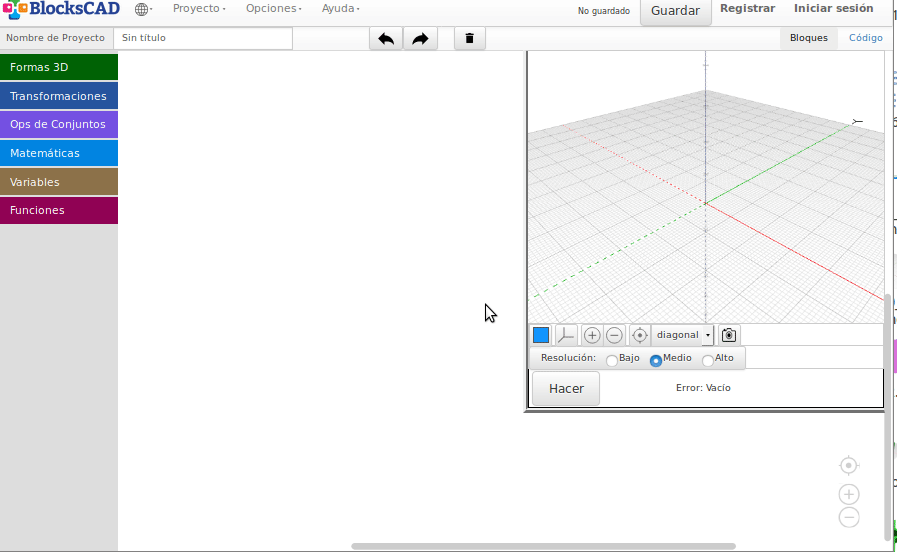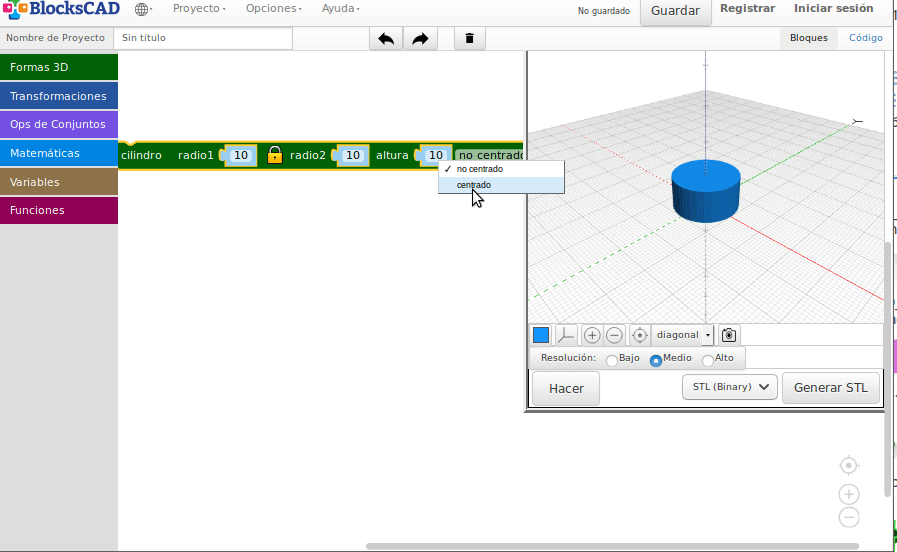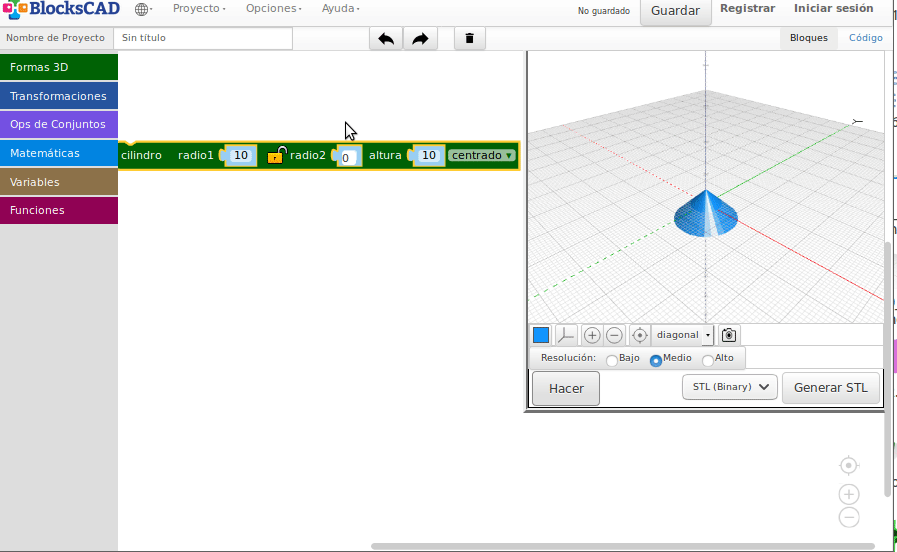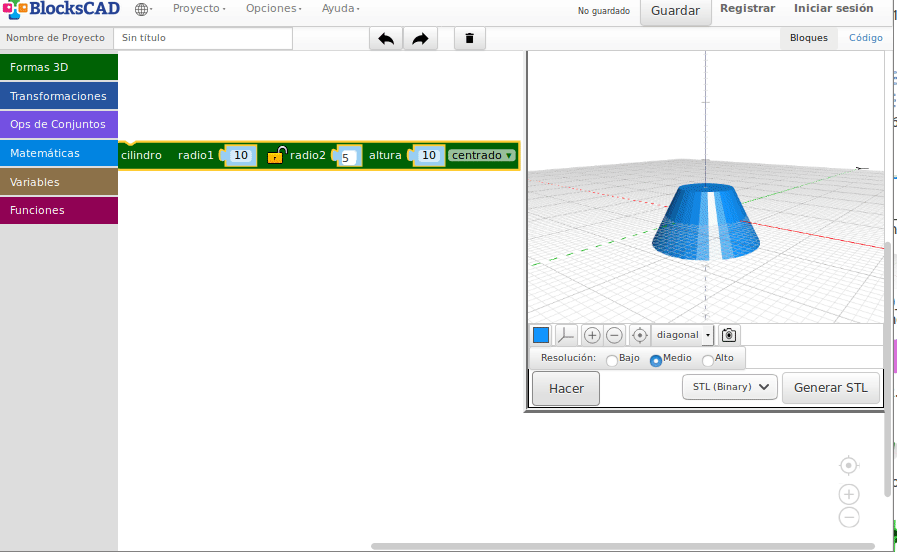
- Cilindros:
- Cilindros
- Conos y troncos
- Prismas y troncos
- Pirámides
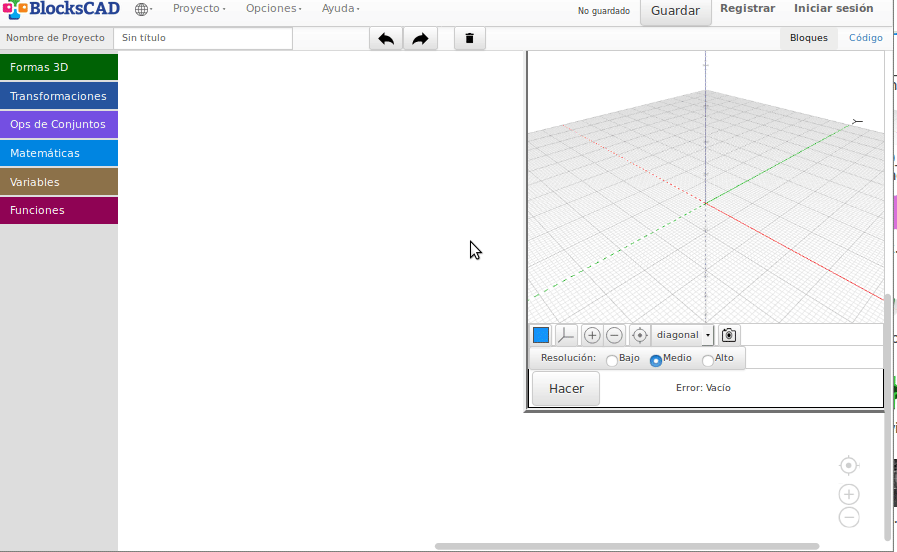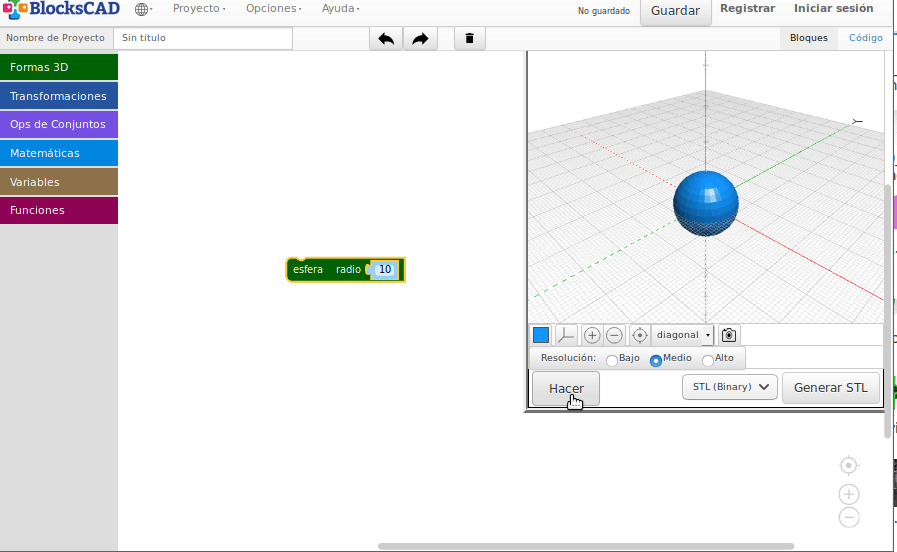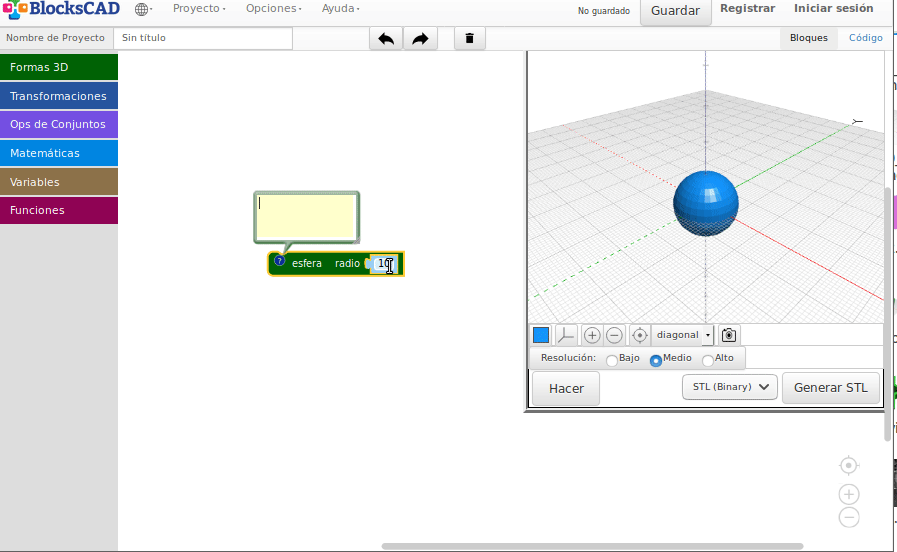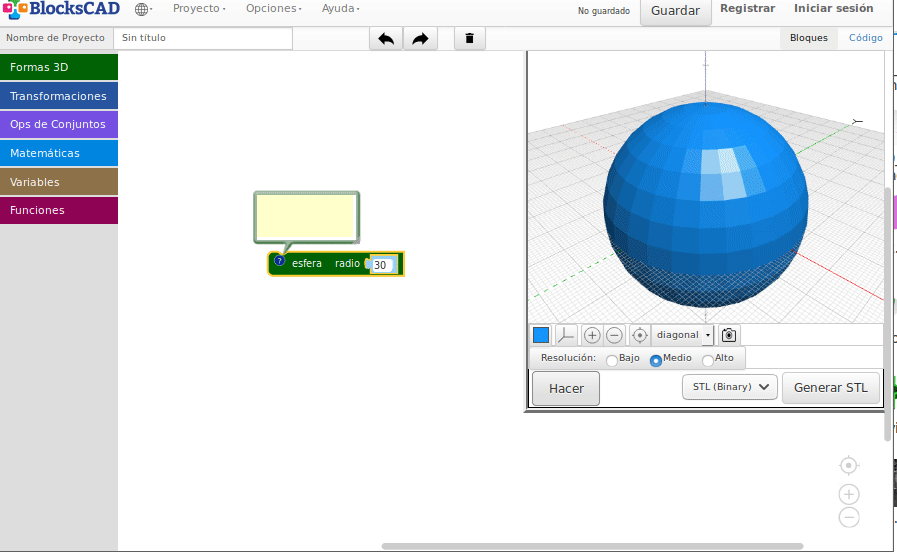
Esferas
Cilindros, conos y troncos
Prismas, pirámides y troncos
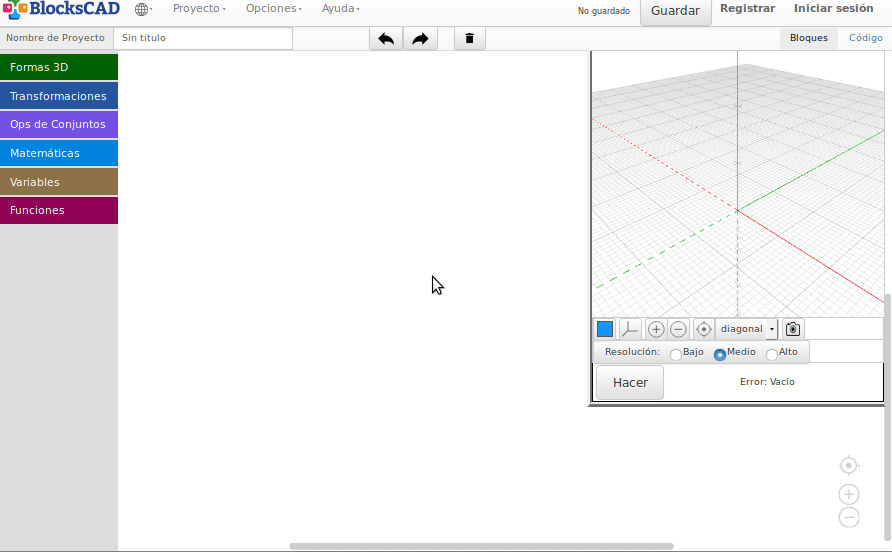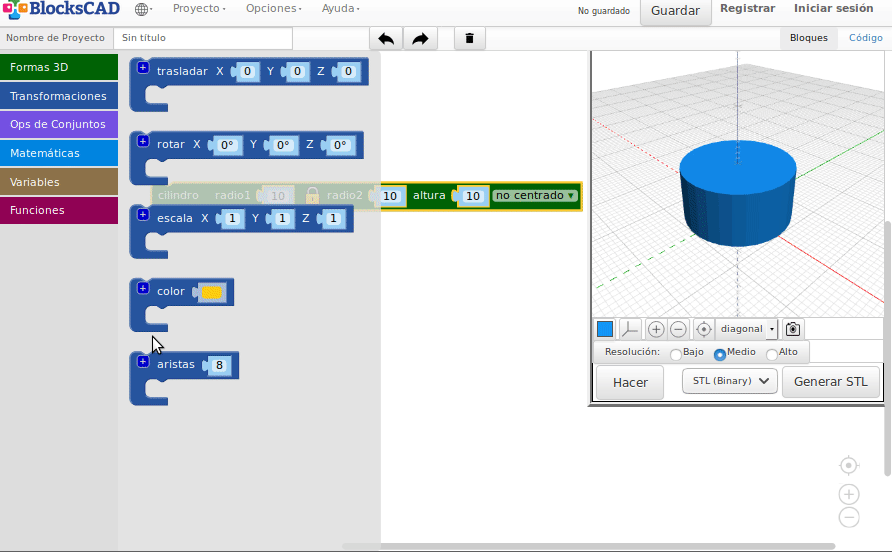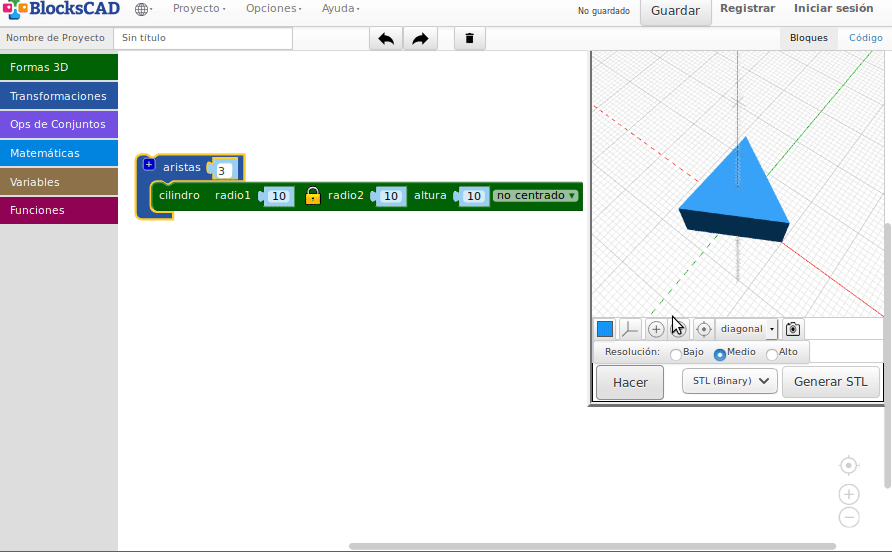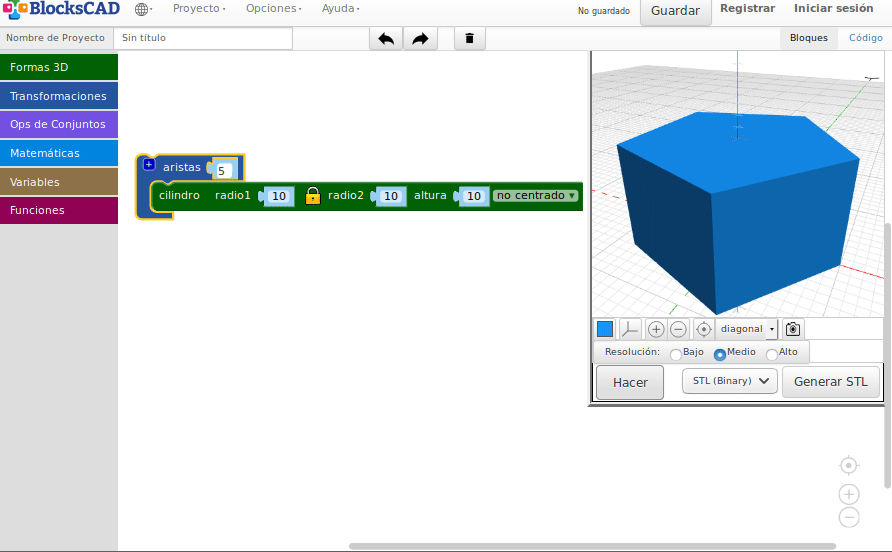
Transformaciones en el espacio
- Traslaciones
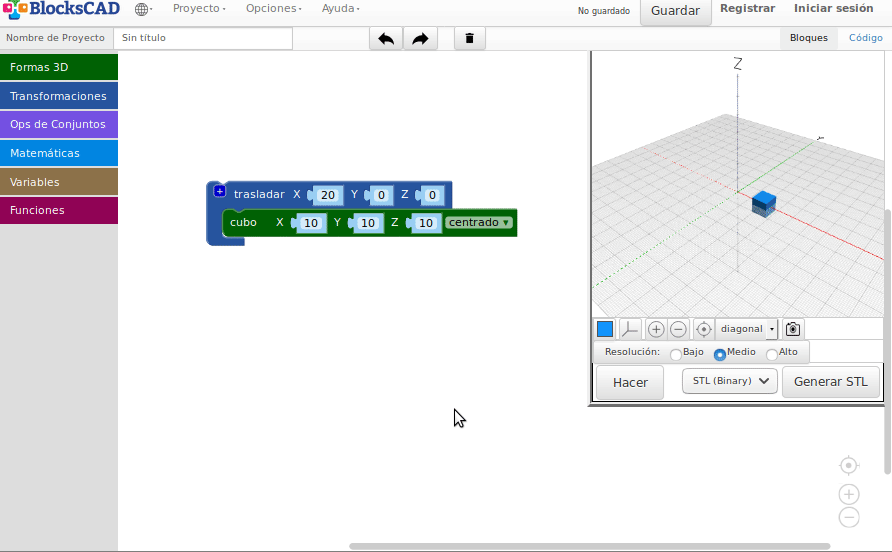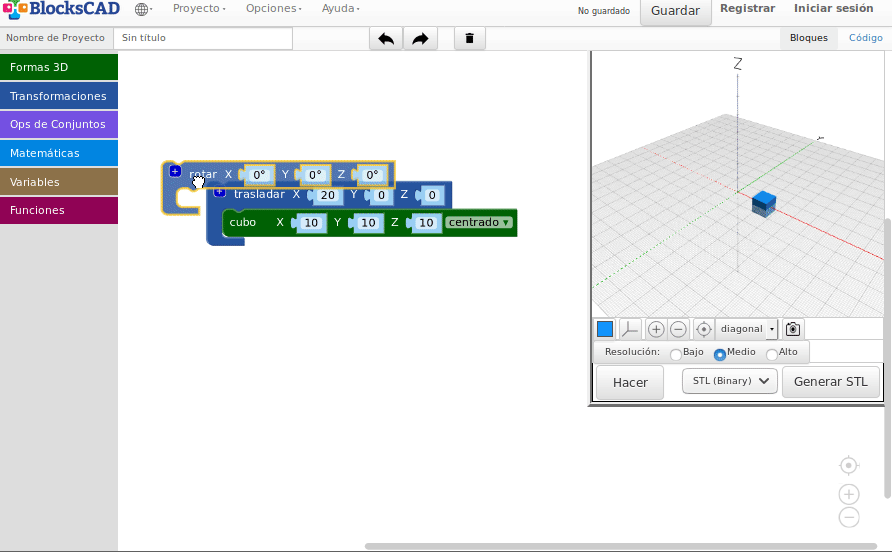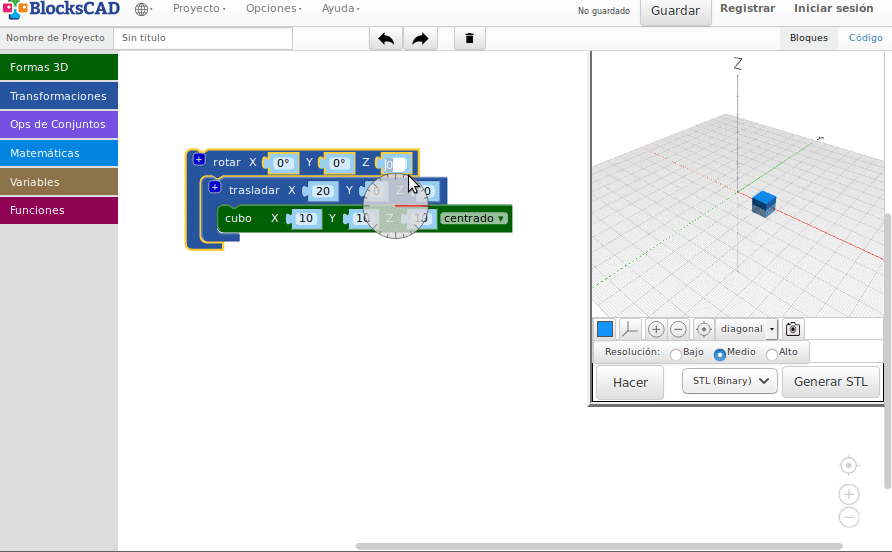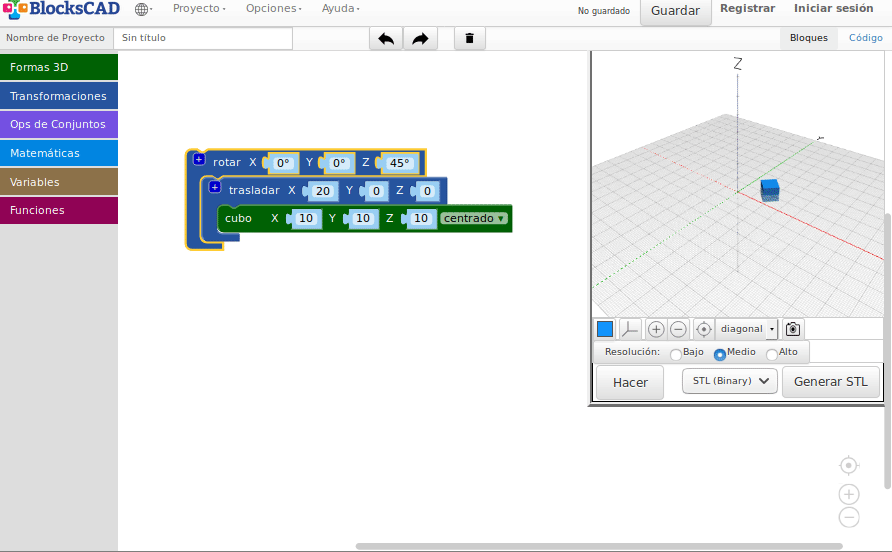
- Rotaciones
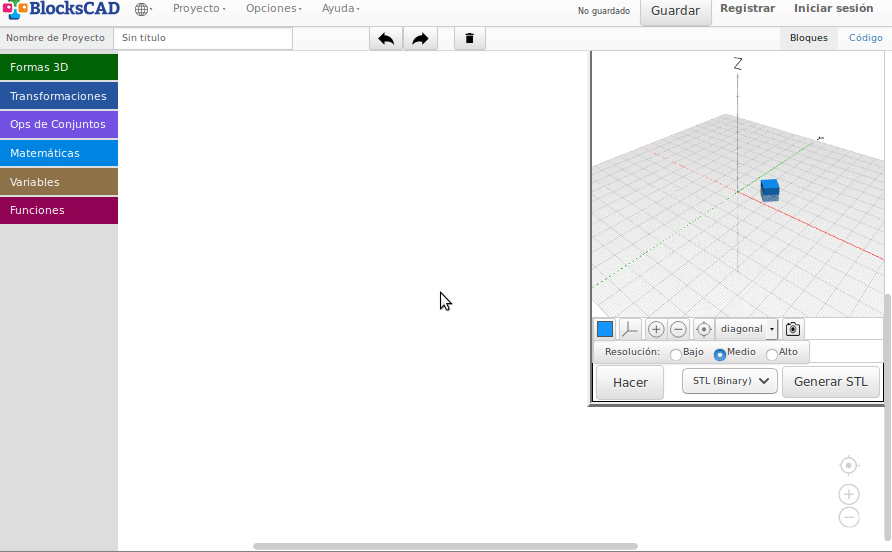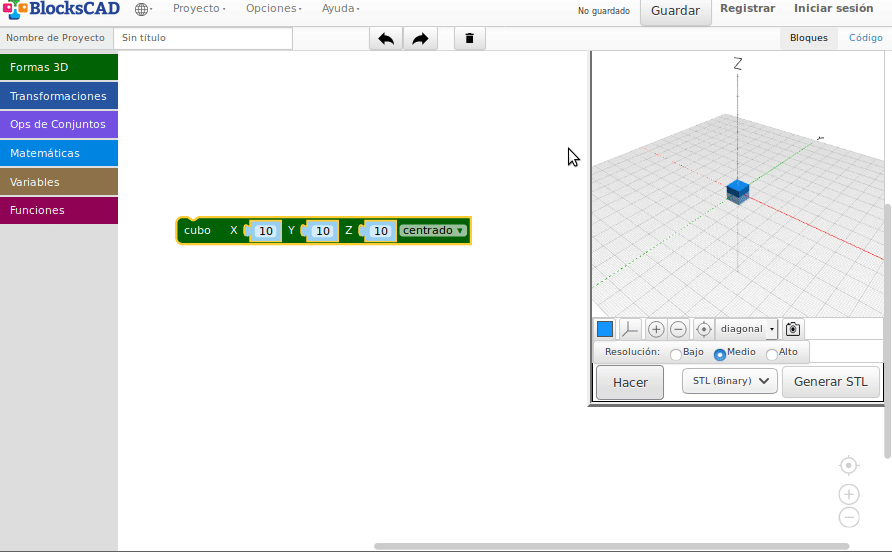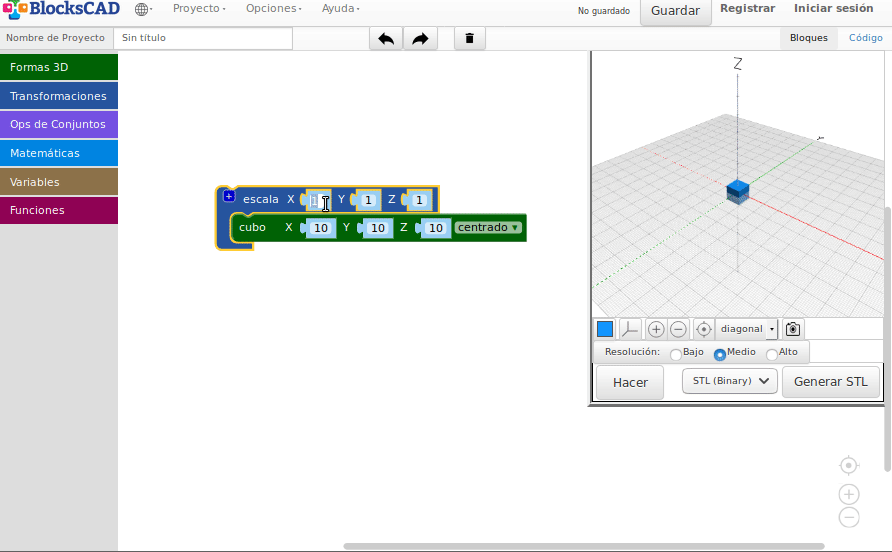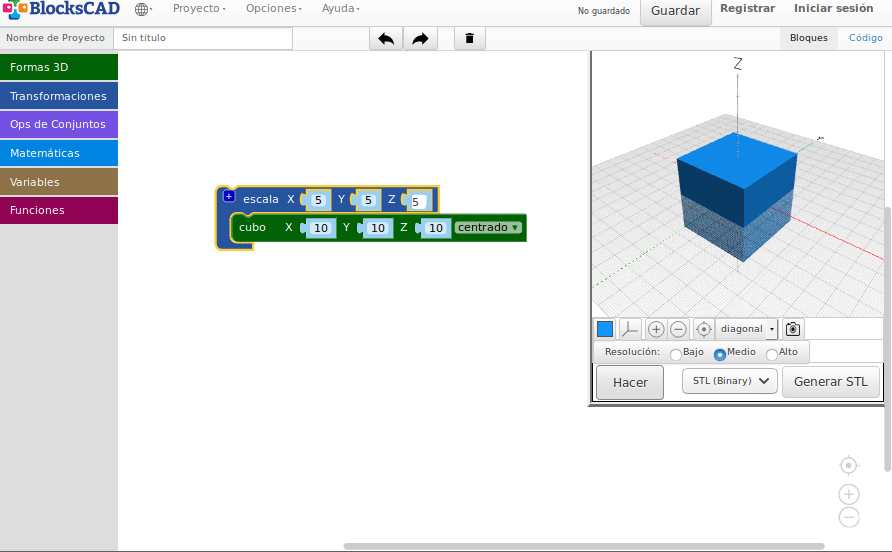
- Escalas
- Simetrías
Traslaciones
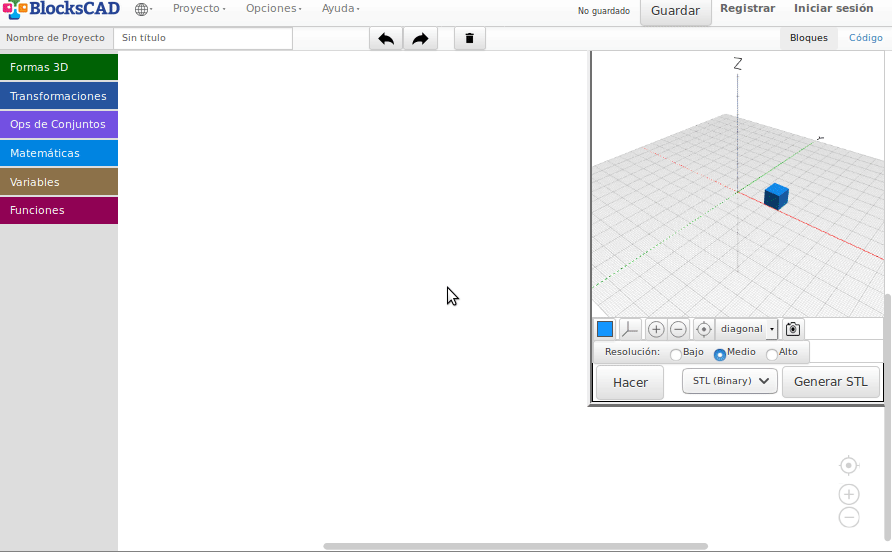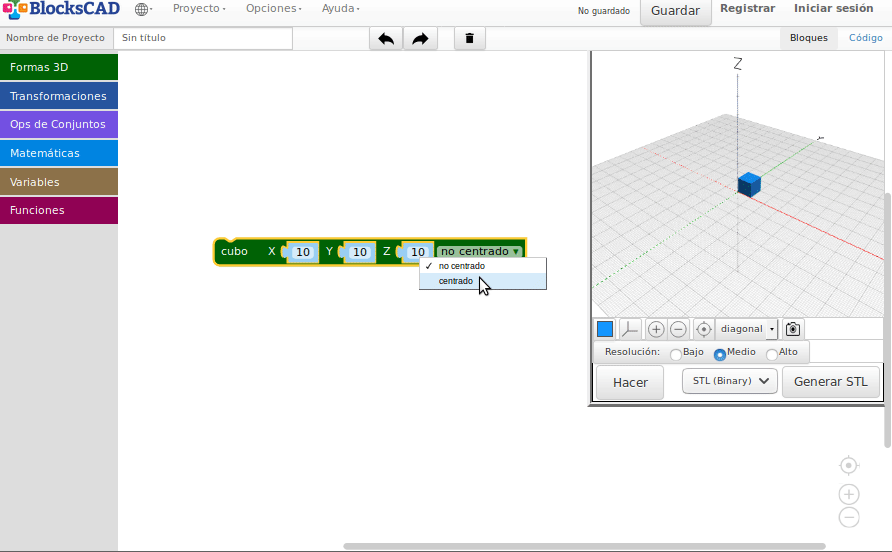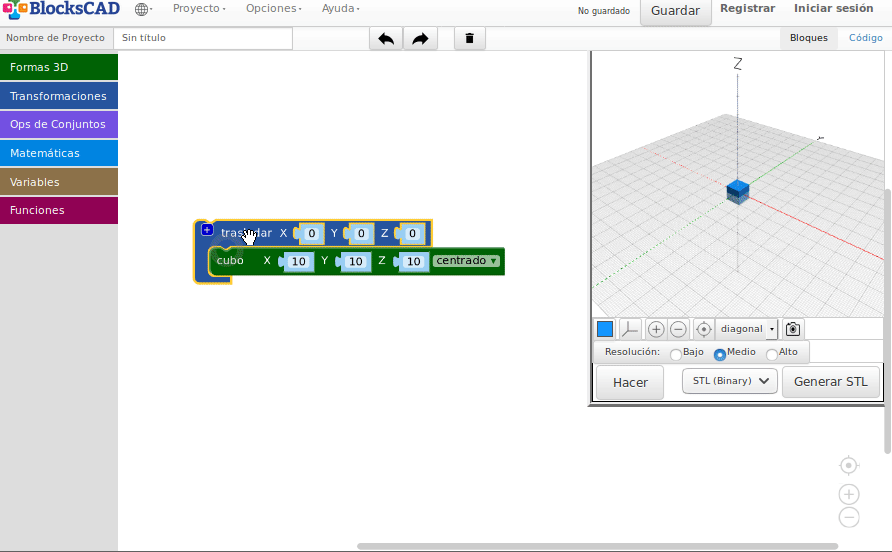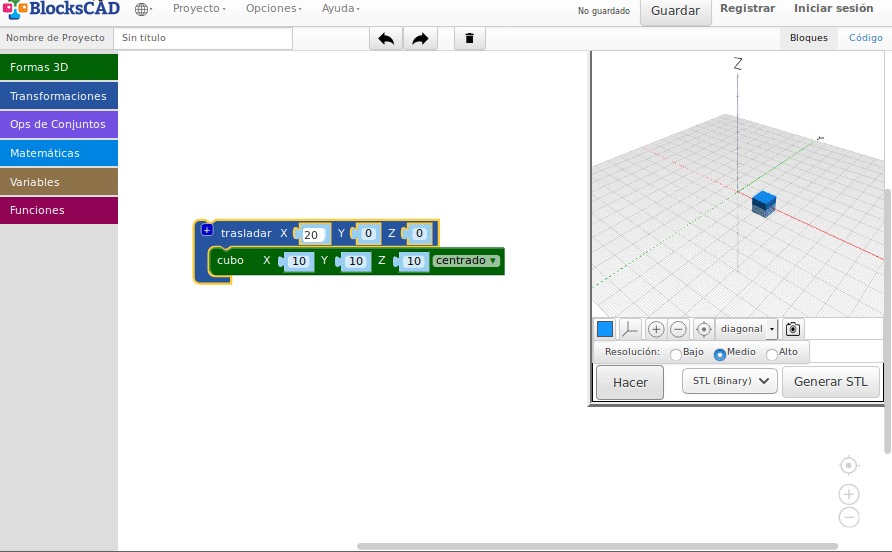
Rotaciones
Escalas
Simetrías
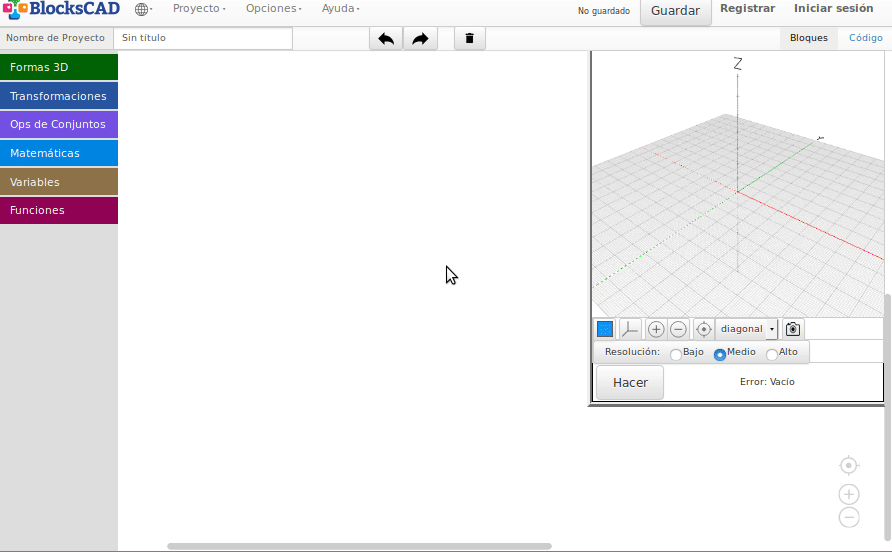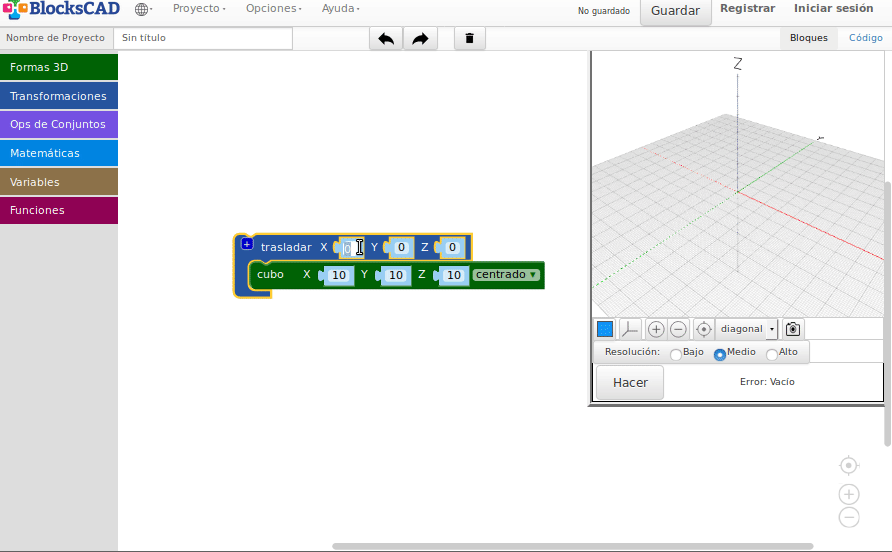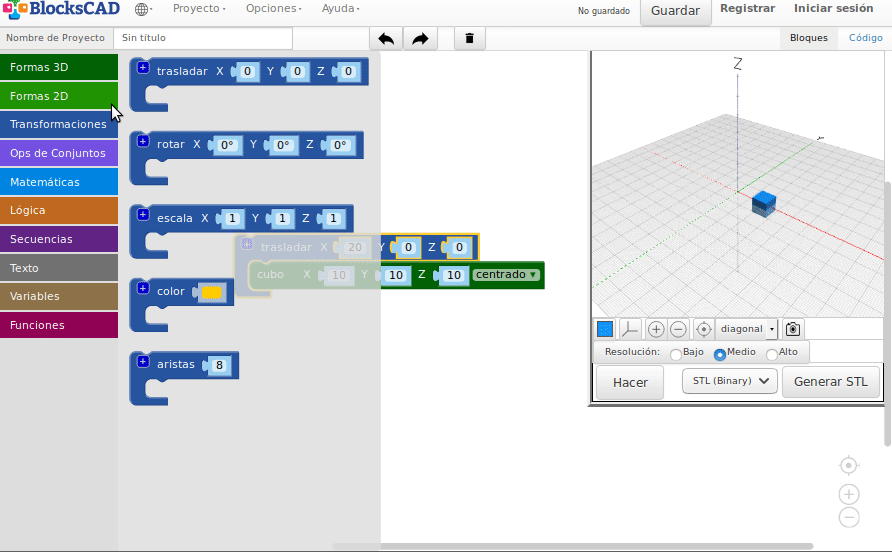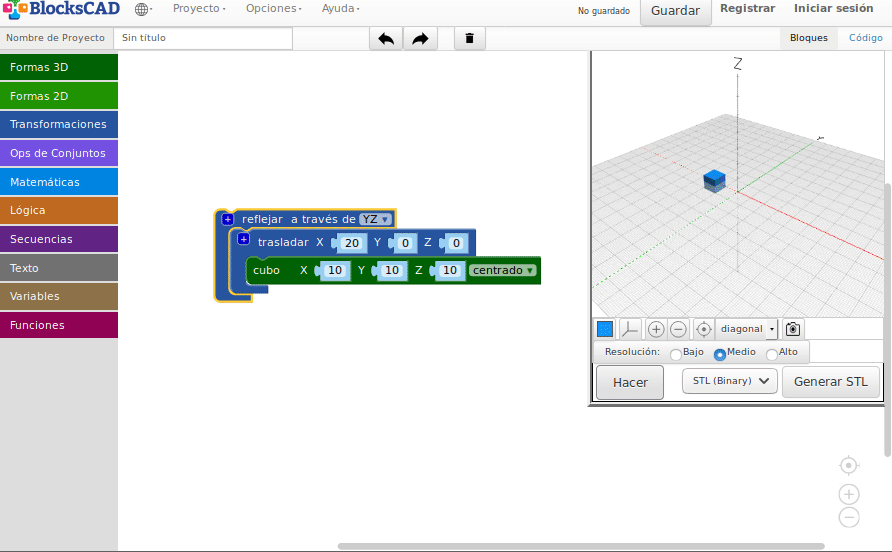
Operaciones de conjuntos (∪,∩, \)
- Unión (Pegar objetos)
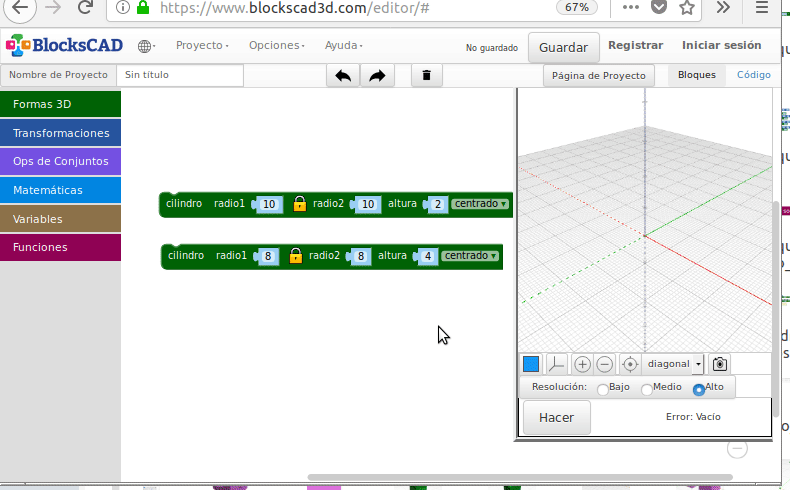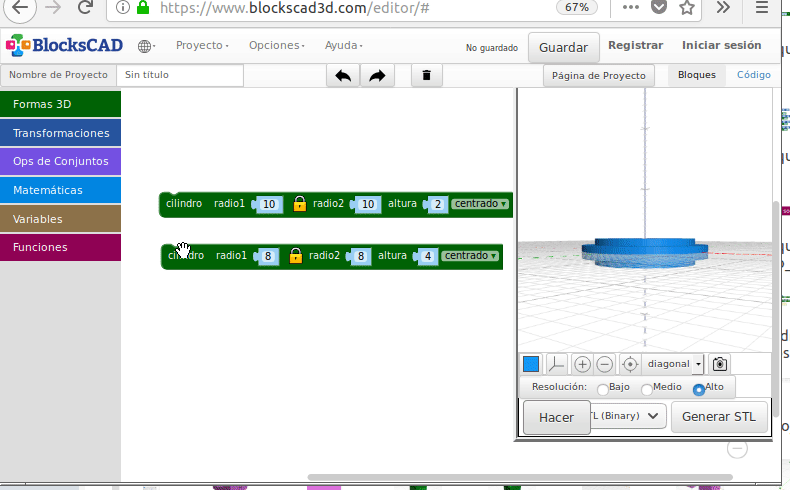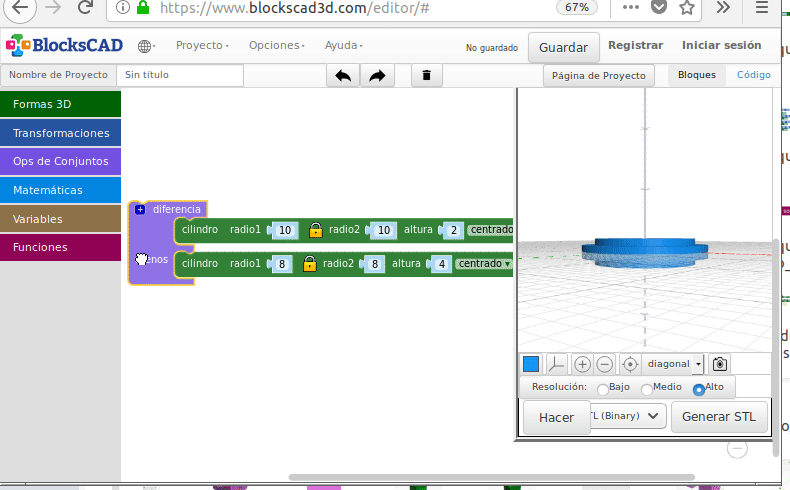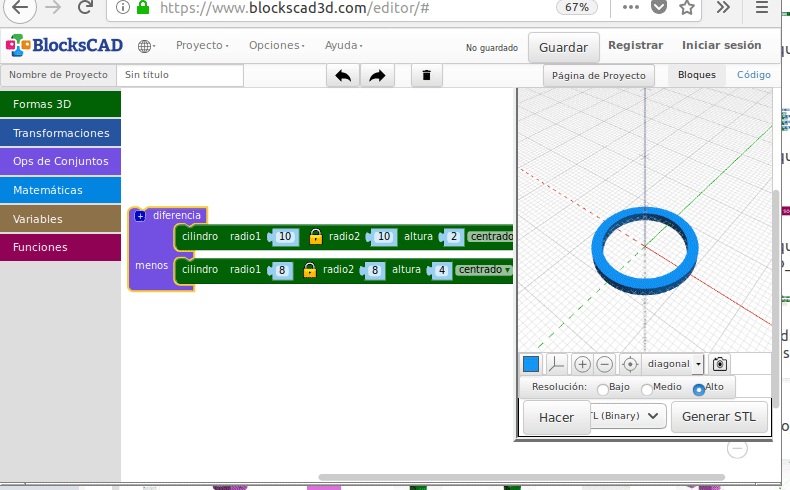
- Diferencia (“Hacer agujeros”)
- Intersección (“Zonas comunes”)
Unión
Diferencia
Intersección
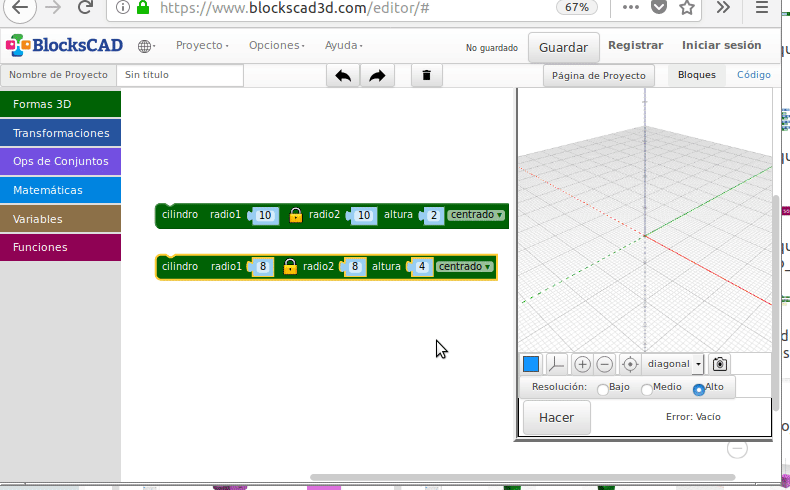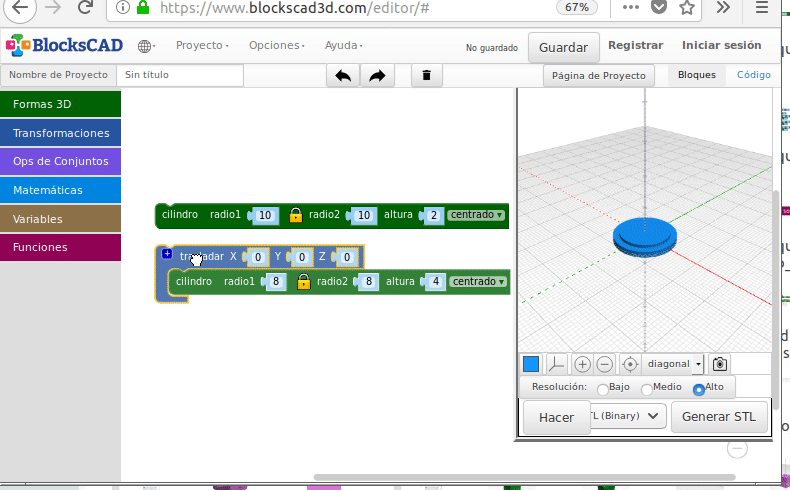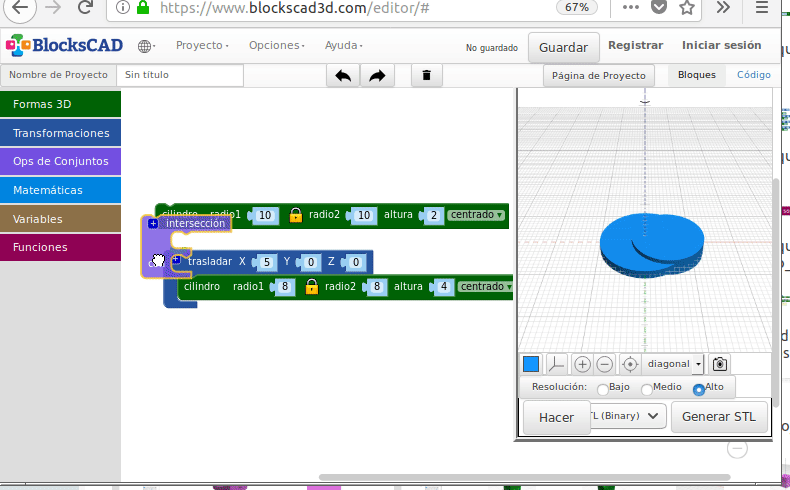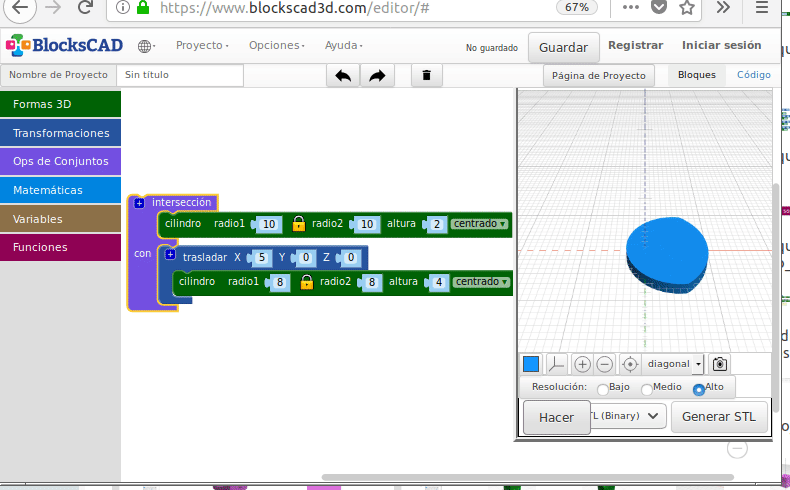
¡Ya sabes lo básico para manejarte con BlocksCAD!
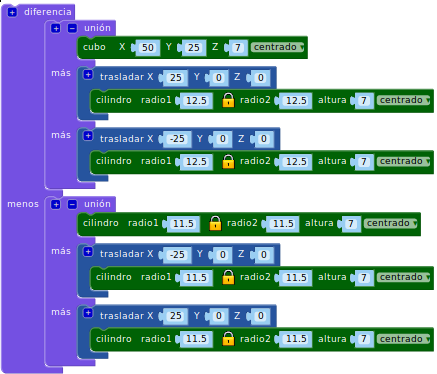
Actividad propuesta: Spinner
Modela un spinner de dos ramas con tres agujeros para cilindros de radio 11mm y 7 mm de altura. Tienes que conseguir algo parecido a esto:
Posible solución
BlocksCAD “avanzado”
Variables
- Una variable es un contenedor de datos
- Los datos serán medidas
- Permiten parametrizar objetos
Operaciones matemáticas
- Operaciones matemáticas con las medidas y los valores de las variables
Bucles o repeticiones
- Repetición de un conjunto de bloques
- El número de repeticiones se controla con una variable a la que llamaremos contador
Funciones
Permiten encapsular un conjunto de bloques en otro
al ejecutar la función ejecutaremos internamente los bloques encapsulados
Actividad propuesta:
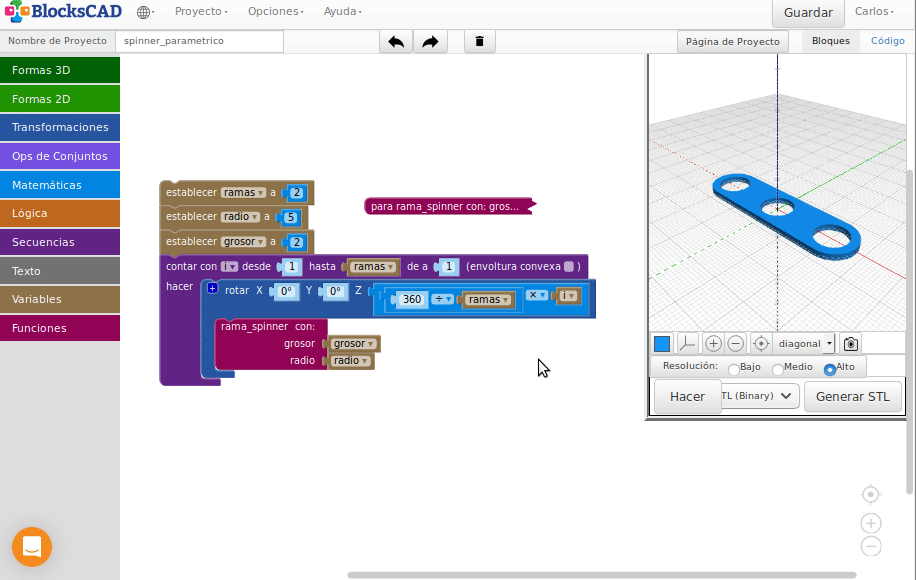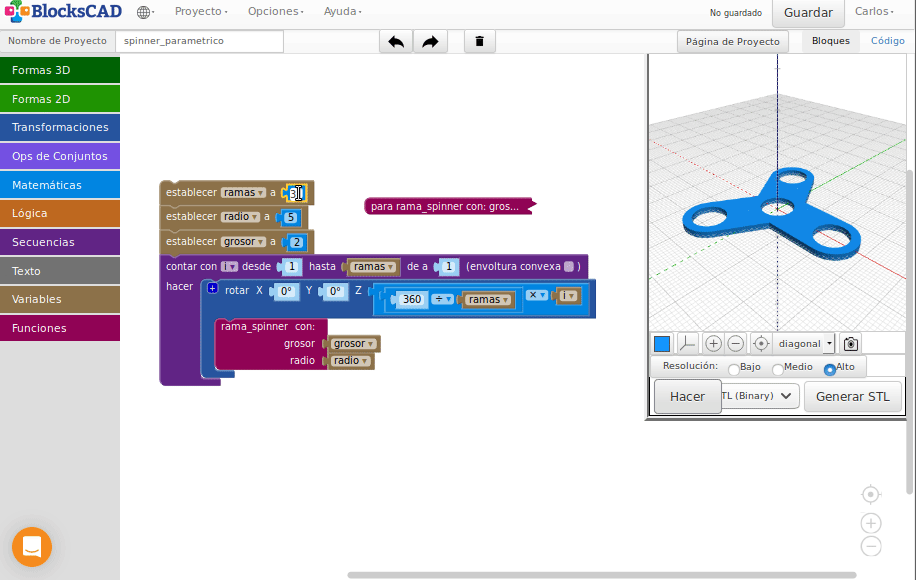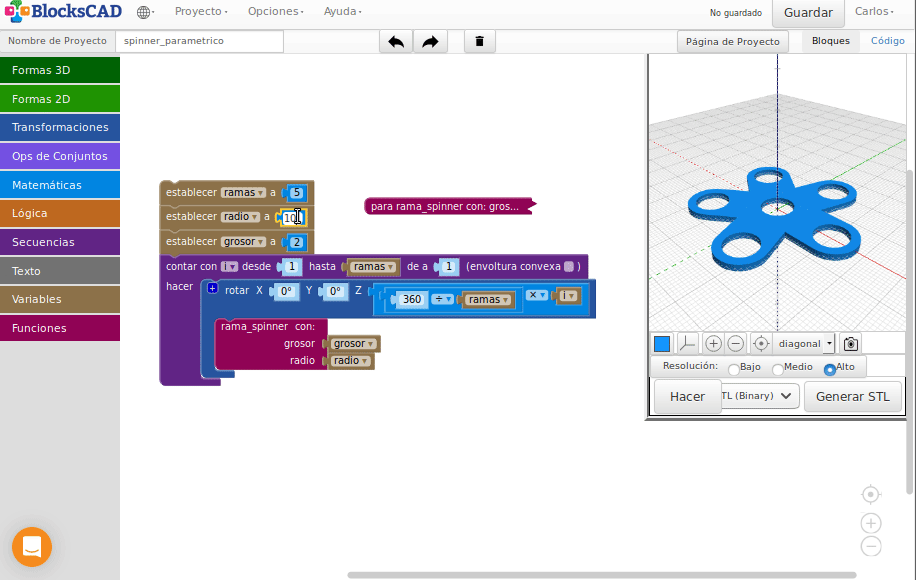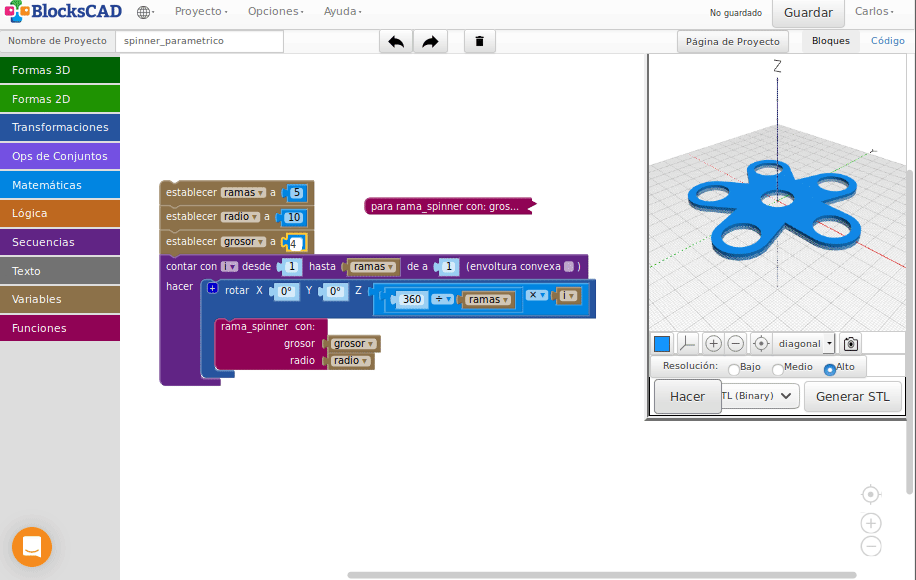
Spinner paramétrico
Realiza un spinner de dimensiones “variables” donde se pueda elegir el tamaño del agujero, el grosor del spinner y el número de ramas
Crea una función que genere una rama
Repite la función anterior haciendo el giro que corresponda para obtener el spinner deseado
El resto de las medidas se dejan a criterio del diseñador, pero que queden proporcionales

Inspírate: Desafío 1
Estrella mudéjar
Modela el objeto de la derecha:
- La estrella mudéjar es un elemento decorativo ampliamente utilizado desde tiempos remotos por diferentes civilizaciones mediterráneas.
- En Aragón resulta un ornamento muy característico del mudéjar
- Aparece al superponer los centros de dos cuadrados idénticos pero uno girado 45º con respecto al otro
Estrella mudéjar 2
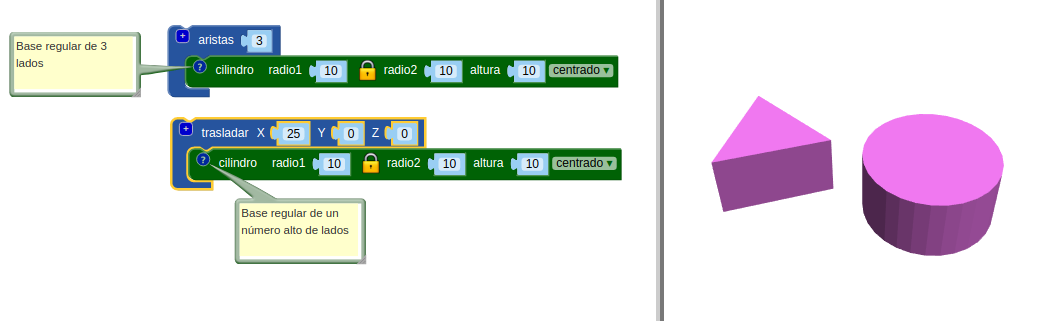
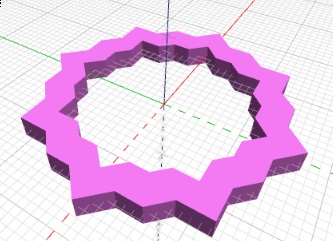
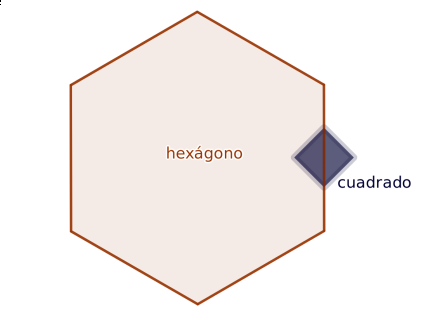
Modela el objeto de la derecha con el número de lados como parámetro:
La mitad de las puntas las tienen que generar un prisma cuadrado con la diagonal superpuesta sobre la arista (el lado del cuadrado se pide que sea 1/3 de la arista).
Como una imagen vale más que mil palabras:
Inspírate: Desafío 2
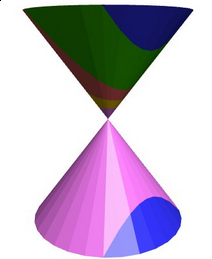
Cono de Apolonio
Modela un cono como el que aparece a la derecha y practica con las secciones de un cono
- Al cortar con un plano diferentes puntos del cono obtenemos un serie de curvas planas llamadas cónicas. Las diferentes curvas reciben los siguientes nombres:
- círculo: corte con un plano paralelo a la base del cono
- elipse: corte oblícuo con respecto a la base e inclinación menor a la generatriz del cono (siendo el ángulo de inclinación el que forma el plano con el plano normal al eje de simetría del cono)
- parábola: corte de un plano paralelo a una generatriz del cono
- hipérbola: corte oblícuo con respecto a la base e inclinación mayor a la generatriz del cono