Taller de Talento Matemático¶

Programando la Geometría con BlocksCAD¶
Página Web: https://mat3d.github.io/
Documentación: https://github.com/mat3d
Introducción¶
- Saludo y presentación
- Pablo Beltrán Pellicer @pbeltranp
- Carlos Rodríguez Jaso @es3a10
- Objetivo de la sesión:
- Iniciarse en las posibilidades de BlocksCAD desde un punto de vista matemático
Introducción a BlocksCAD¶
BlocksCAD es un programa para modelar objetos en 3D sin necesidad de tener elevados conocimientos de programación.
La forma más sencilla de trabajar es de manera online a través de su web: https://www.blockscad3d.com/
Formas 3D: Esferas¶
Dentro del bloque Formas 3D podemos arrastrar el bloque 
Al renderizarlo obtendremos una esfera de 10mm de radio:

Formas 3D: Cilindros y mucho más¶
Dentro del bloque Formas 3D, tenemos el bloque 
Explicación de algunos parámetros:
- radio1, es el radio de la base inferior de la figura a modelar
- candado, por defecto aparece cerrado, y esto hace que el parámetro radio2 herede el valor de radio1
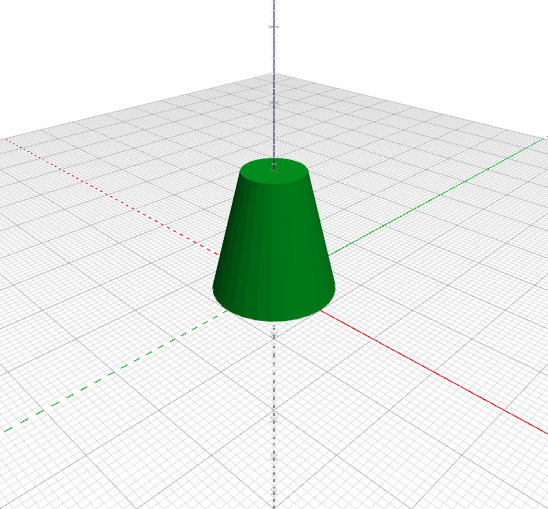
- radio2, radio de la base superior de la figura. Cuando coincida con radio1 tendremos un cilindro, y cuando no, tendremos un tronco de cono o un cono si ponemos que el radio es cero
Ejemplos:
| Bloque | Renderizado |
|---|---|
 |
 |
 |
 |
 |
 |
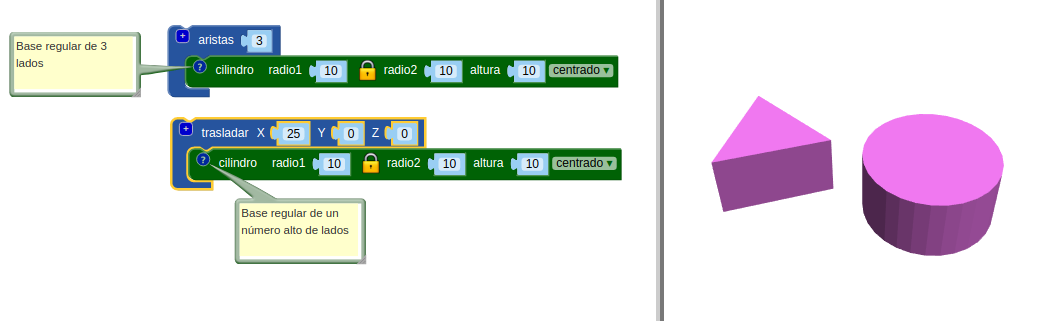
BlocksCAD interpreta la base del cilindro como un polígono regular de "muchos" lados. Podemos generar un prisma de base regular modificando ese "muchos" con el bloque 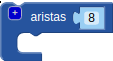 que aparece en Transformaciones. Mira este ejemplo que compara un cilindro con un prisma de base triangular:
que aparece en Transformaciones. Mira este ejemplo que compara un cilindro con un prisma de base triangular:
Transformaciones¶
Traslaciones¶
Dentro del bloque Formas 3D, arrastramos el bloque  En este caso, los parámetros X, Y y Z, son las coordenadas del vector de traslación.
En este caso, los parámetros X, Y y Z, son las coordenadas del vector de traslación.
Rotaciones¶
Bloque 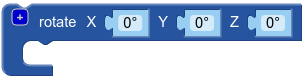 Los parámetros X, Y y Z, son los grados a rotar en los diferentes ejes.
Los parámetros X, Y y Z, son los grados a rotar en los diferentes ejes.
Ejemplos:
| Ejemplo | Bloque | Renderizado |
|---|---|---|
| Prisma de 10x20x30 centrado y trasladado 30 en la dirección X, 30 en la Y y 40 en la Z | 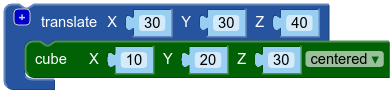 |
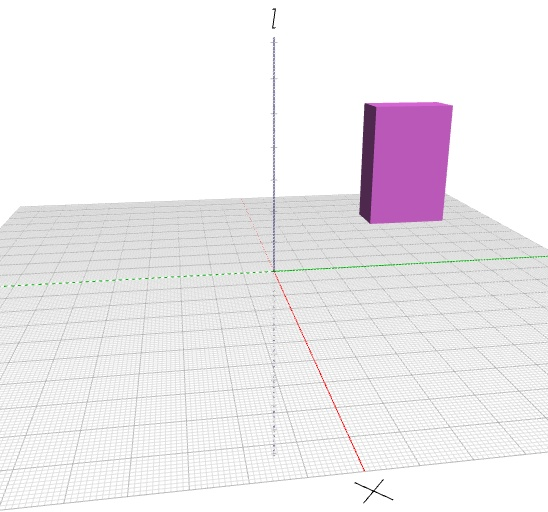 |
| Ejercicio anterior rotado 45º en el eje X | 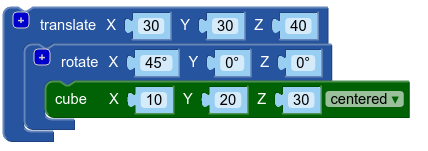 |
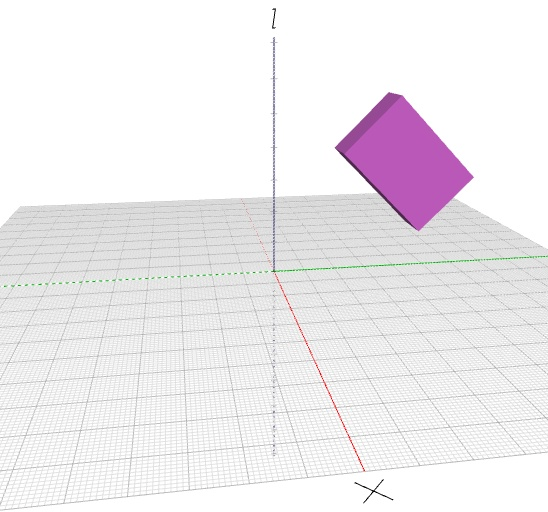 |
¡Ya conoces lo básico para poder trabajar!¶

Desafío 1:¶
Entrénate con BlocksCASD intentando modelar la siguiente figura. No tiene que ser exactamente igual pero sí parecida:
| Vista 1 | Vista 2 |
|---|---|
 |
 |
Tienes una posible solución en https://www.blockscad3d.com/community/projects/82576
Desafío 2: Estrella Mudéjar¶
| Actividad |
|---|
| Estrella mudéjar sencilla |
| "Estrella mudéjar" sobre un hexágono regular |
| "Estrella mudéjar" paramétrica sencilla |
| "Estrella mudéjar" paramétrica avanzada |
Cuestiones iniciales¶
- ¿Existe alguna relación entre el lado de un cuadrado y su apotema?
- ¿Crees que para otros polígonos regulares va a seguir existiendo una relación entre el lado y la apotema?
- ¿Sabes algo de trigonometría? En caso afirmativo, las preguntas anteriores deberían resultarte sencillas. En caso contrario, no te preocupes la parte teórica la facilitaremos para que puedas hacer el modelado si te ves desbordado.
Respuestas a las preguntas¶
La apotema es la mitad del lado.
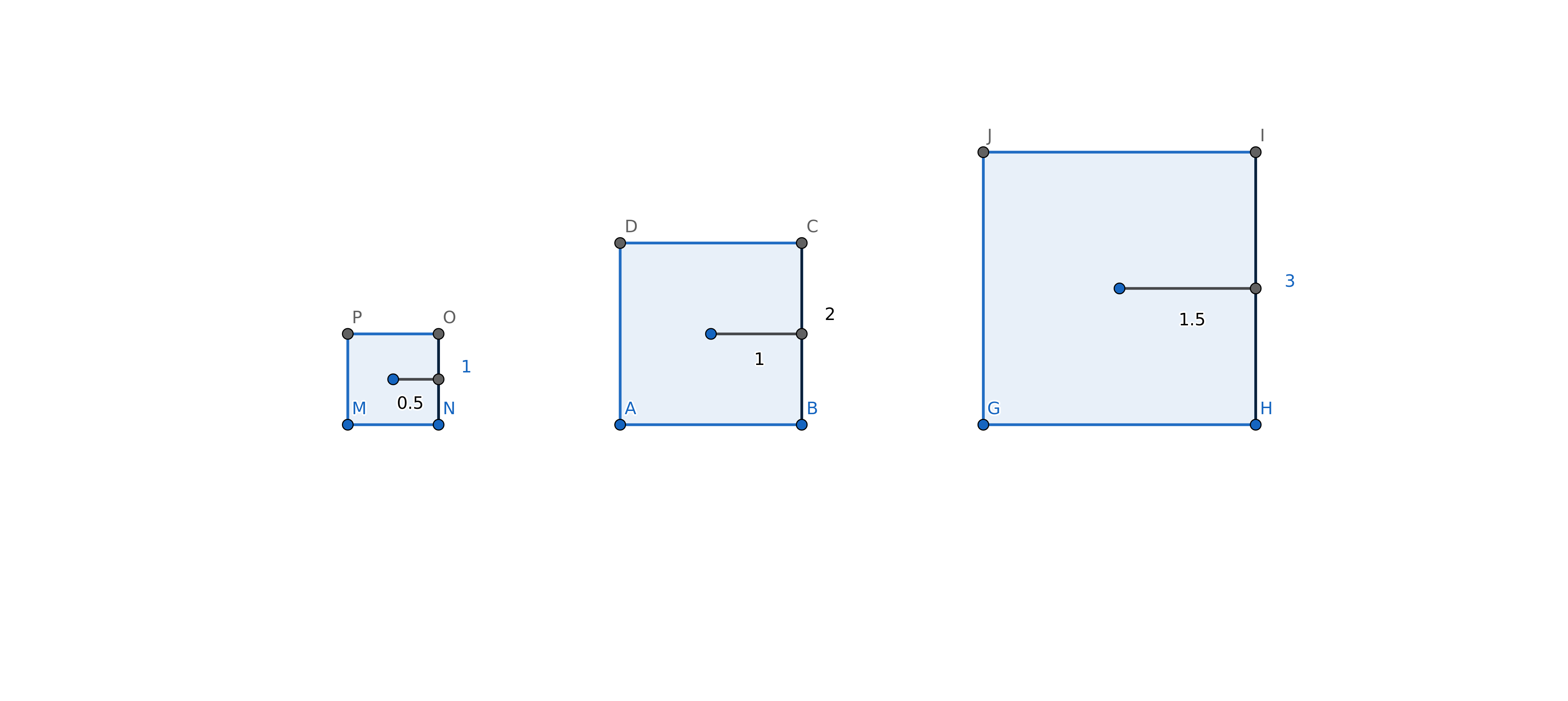
Sí, siempre va a haber relación. La respuesta está en la semejanza de triángulos rectángulos y la trigonometría. Esto nos permitirá calcular bien el radio, la apotema o el lado del polígono regular siempre que nos den uno de ellos.
Modelado en BlocksCAD¶
| Paso | Código | Renderizado |
|---|---|---|
| Insertamos un cubo de 10x10x5 centrado en origen |  |
 |
| Insertamos otro igual pero girado 45º sobre el plano XY (girar el eje Z) | 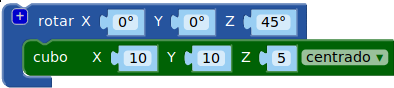 |
 |
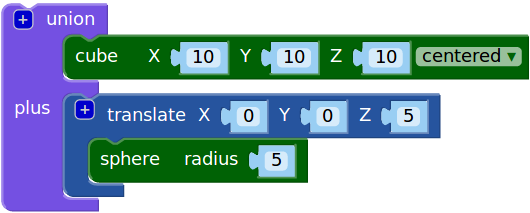
| Juntamos los dos objetos para formar un único objeto | 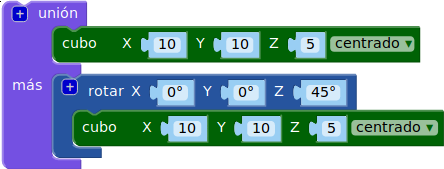 |
 |
Tienes la solución en https://www.blockscad3d.com/community/projects/266387
Cuestiones previas¶
- ¿Hacia qué objeto tiende un polígono regular cuando aumentamos el número de lados al polígono?
- ¿Cuánto tiene que girar el prisma hexagonal superpuesto para generar las puntas en mitad de las aristas del prisma original?¿Puedes dar una fórmula general que vaya en función del número de lados y que por tanto sirva para el cuadrado o el hexágono?
Consideraciones a las cuestiones¶
Al aumentar el número de lados, el polígono se va acercando a un círculo como se puede ver en la siguiente animación:

BlocksCAD interpreta los cilindros de esta manera, como un prisma de base regular con un número de lados elevado. Podemos convertir un cilindrode BlocksCAD en un prisma modificando el número de lados:

La rotación que hay que hacer es la mitad del ángulo central: $\alpha=\frac{180}{nlados}$
Importante: Al usar el bloque cilindro modificado por el número de aristas, el parámetro que le damos es el radio del polígono regular y no la longitud de la arista (o lado del polígono regular)
Modelado en BlocksCAD¶
Se propone como ejercicio su modelado.


Tienes una posible solución en https://www.blockscad3d.com/community/projects/272240
"Estrella mudéjar" paramétrica sencilla¶
Modelo¶
Se pide modificar la estrella anterior para que acepte los siguientes parámetros o variables:
- Número de lados del polígono regular que genera la estrella
- Longitud del radio del polígono
- Longitud del radio del polígono que genera el hueco
Ejemplo de modelo: Estrella de David generada con triángulos de radios 10 y 8, exterior e interior respectivamente.

Modelado en BlocksCAD¶
Se propone como ejercicio su modelado.


Tienes una posible solución en https://www.blockscad3d.com/community/projects/278006
"Estrella mudéjar" paramétrica avanzada¶
Modelo¶
Vamos a añadir un poco de complejidad al programa. En las estrellas anteriores todas las puntas son iguales. Ahora en lugar de que la mitad de las puntas las genere el prisma poligonal girado se pide que sean los generados por un prisma cuadrado con la diagonal superpuesta sobre la arista (el lado del cuadrado que sea 1/3 de la arista).
Ejemplo: Para 8 lados tiene que quedar algo así
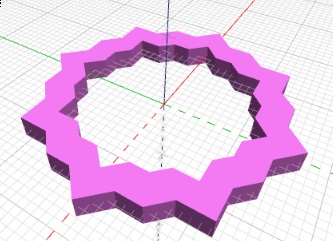
Explicación del Modelo¶
Como una imagen vale más que mil palabras:
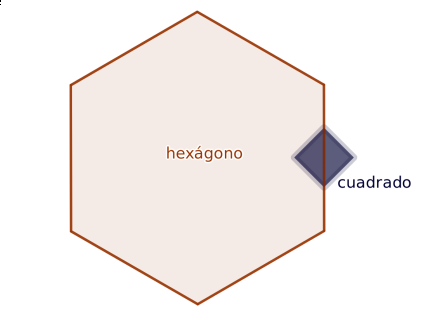
Se pide por tanto modelar una estrella que tenga como parámetros:
- Número de lados
- Longitud del lado
- Grosor de la estrella: Altura y anchura del contorno. Opcional: Si se quiere se pueden hacer dos parámetros.
Cuestiones previas¶
- Dado un polígono regular: ¿Existe alguna fórmula general que relacione la longitud del lado con el radio?¿Y alguna relación entre la apotema y el lado?
- El cuadrado que genera las puntas, ¿Cuánto hay que trasladarlo?
- ¿Cuántas rotaciones hay que hacer del cuadrado para generar todas las puntas?¿Qué ángulo entre ellos?
Respuestas a las cuestiones previas¶
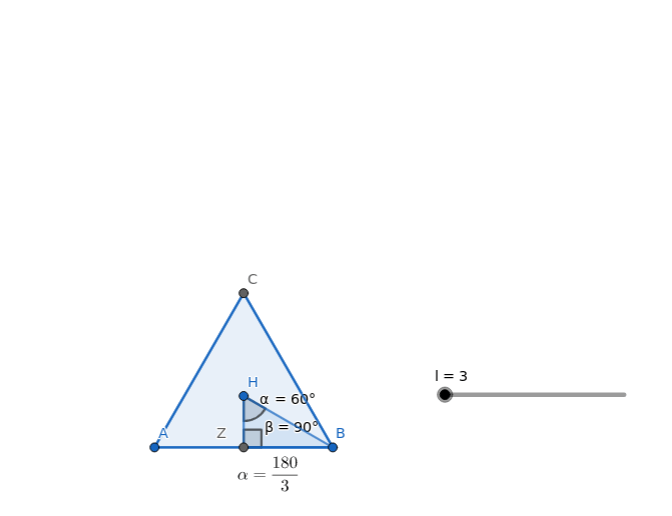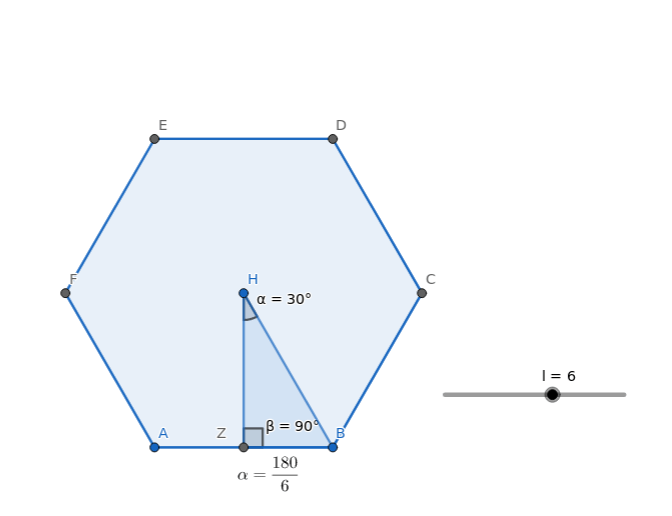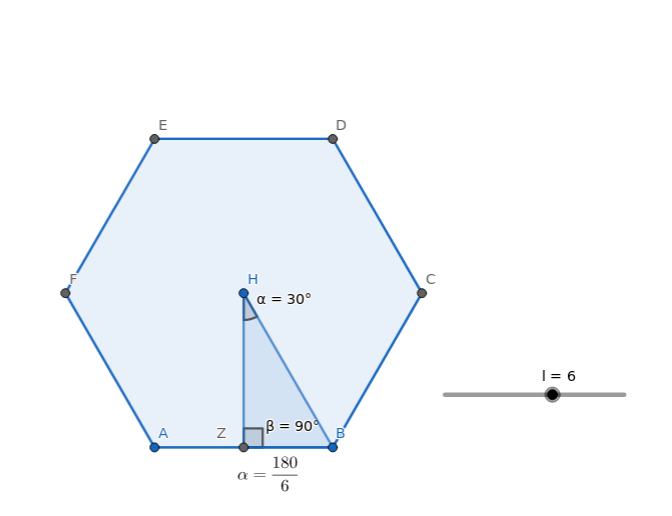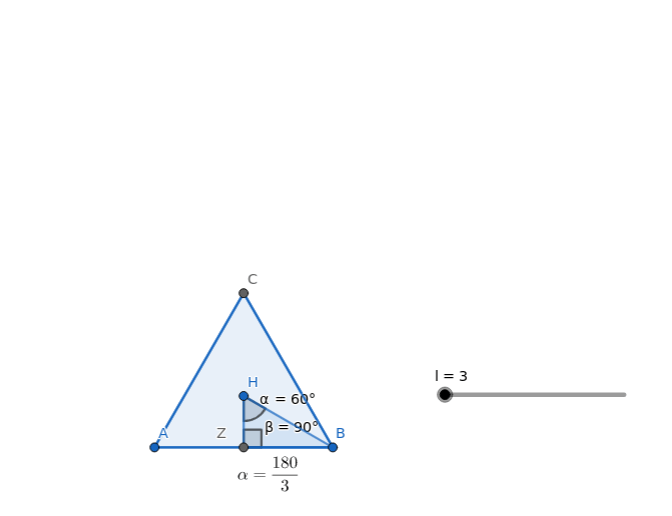
El triángulo formado por el centro del polígono, el punto medio de un lado y un vértice adyacente es siempre rectángulo. El ángulo correspondiente al centro del polígono es la mitad del ángulo central: $$\alpha=\dfrac{\frac{360}{n_{lados}}}{2}$$
Fijado el número de lados del polígono regular, aunque varíe el tamaño del lado, los triángulos que salgan serán semejantes. Al ser semejantes los lados son proporcionales, o dicho de otra forma, la razón entre lados se mantiene constante y dependen exclusivamente del ángulo que se apoya en el centro del polígono: Son las razones trigonométricas. La principales son:
| Razón trigonométrica | Aplicación en el polígono regular |
|---|---|
| seno = lado opuesto / hipotenusa | $\sin{\alpha}=\frac{semilado}{radio}$ |
| coseno = lado contiguo / hipotenusa | $\cos{\alpha}=\frac{apotema}{radio}$ |
| tangente = lado opuesto / lado contiguo | $\tan{\alpha}=\frac{semilado}{apotema}$ |
- El cuadrado hay que trasladarlo la apotema del polígono
- Habrá que hacer tantas puntas como lados y habrá que rotar la mitad del ángulo central: $$\alpha=\frac{180}{nlados}$$
Ejemplo de aplicación: Determina el radio y la apotema para un pentágono regular de lado 6:
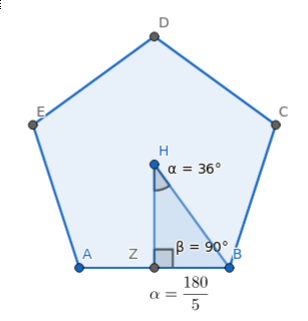
- radio = (6/2)/seno(180/5)
- apotema = (6/2)/tan(180/5)
Modelado en BlocksCAD¶
Se propone como ejercicio su modelado.


Tienes una posible solución en https://www.blockscad3d.com/community/projects/267149
¡Gracias por vuestra presencia y a seguir modelando con BlocksCAD!¶
Podéis seguir trabajando en vuestra casa y difundir vuestros progresos en:
Otros enlaces que pueden ser interesantes:
- Tutoriales de BlocksCAD oficiales
- Proyecto RepRap sobre impresoras 3D libres
- Proyecto Clone Wars , subproyecto de RepRap en castellano
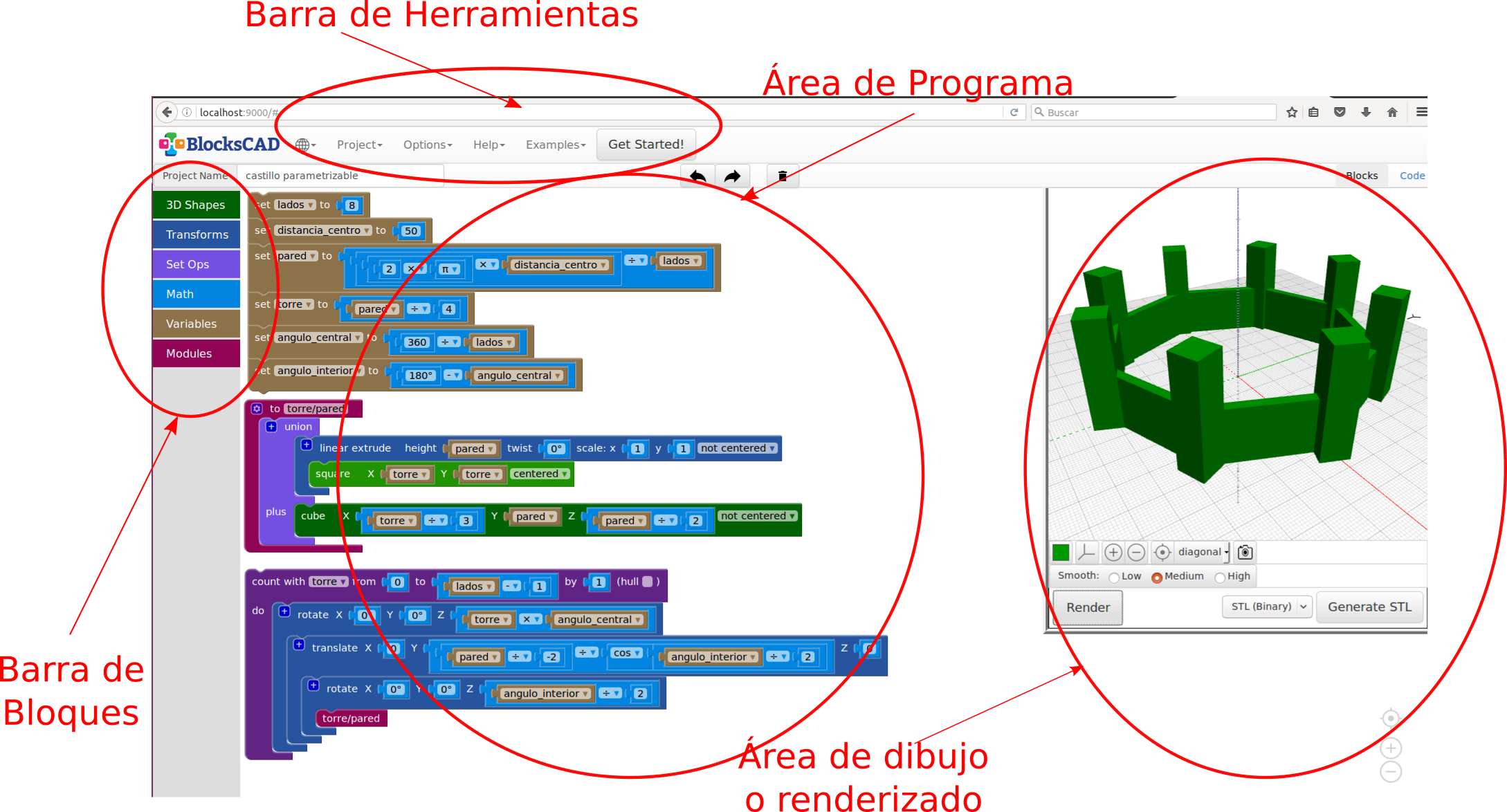
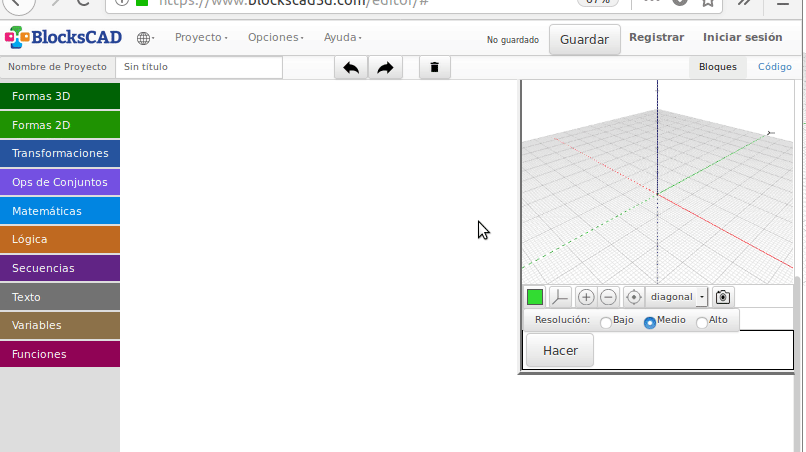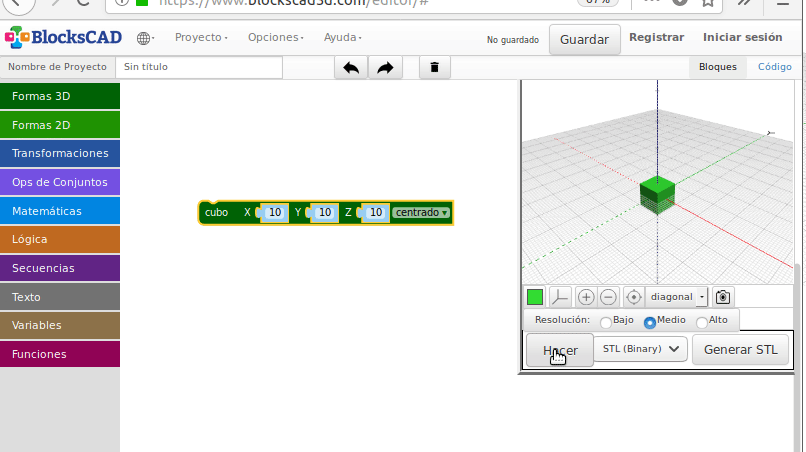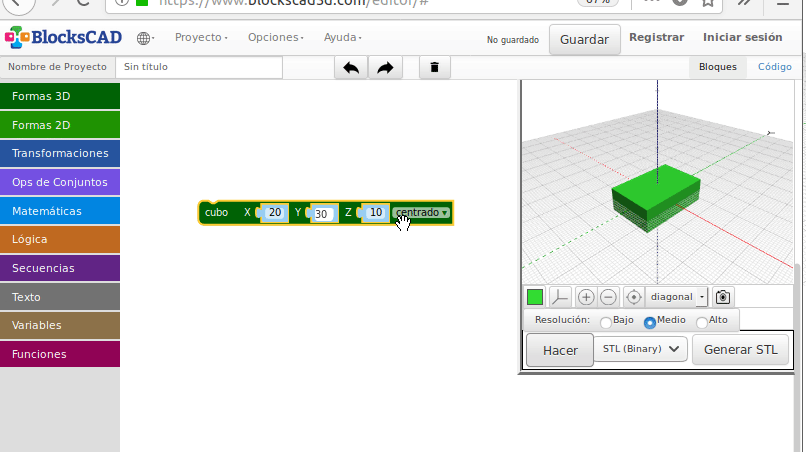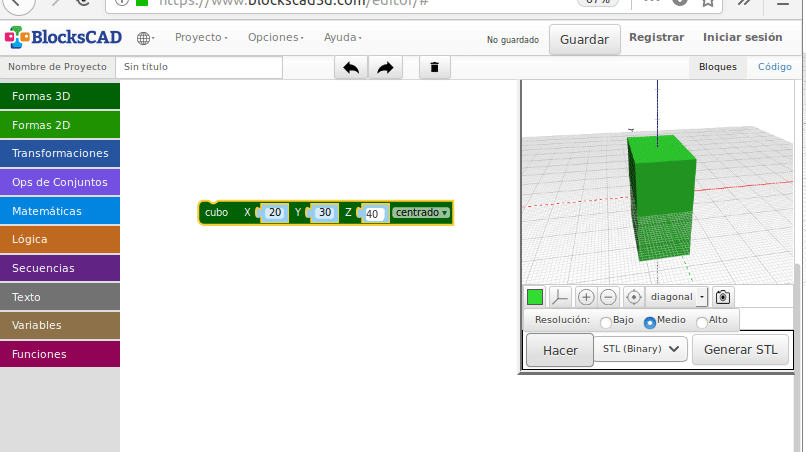
 y lo llevamos a la área de programa. Al renderizar (botón Hacer) ya tenemos nuestro primer objeto con BlocksCAD.
y lo llevamos a la área de programa. Al renderizar (botón Hacer) ya tenemos nuestro primer objeto con BlocksCAD.